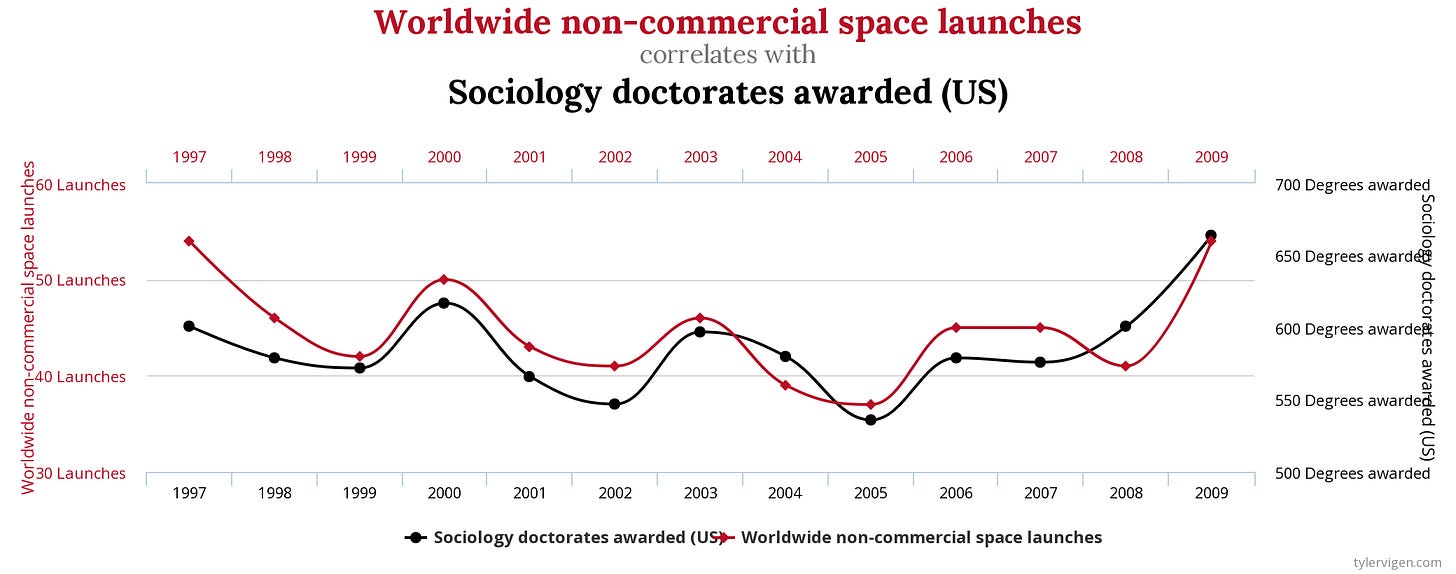
Megapost about causality: the summary of "The Book of Why" by Pearl and Mackenzie and more ideas

Statistics, causality, causal modelling, mediation analysis, counterfactuals, philosophy of research, causal representation learning, ethical AI, the power of abstractions, and systems thinking

Judea Pearl’s and Dana Mackenzie’s The Book of Why is a theoretical and practical book about epistemology, intertwined with history of science (particularly, the history of thinking about causality and causal inference and the application of these ideas in science). The explicit focus of the book is practical epistemology (that is, how researchers should pose questions, conduct research, and publish their results) and the theoretical part, the philosophy of science, is not the explicit focus, but I think it’s worth as much attention as the practical part.

Here and below, I refer to Judea Pearl as the sole author of the book because the book itself is written in first person, where “I” stands for “Judea Pearl”.

Pearl’s grand crusade in The Book of Why is putting to rest the idea that the notion of causality should be avoided in science, and that research questions can always be answered by just running experiments (or observational studies) and then applying some smart statistical procedures to the results, without using, however, any assumptions about the causal relationships between the variables (objects, events, etc.) beyond the obvious “assumption” that events that have happened later in time couldn’t cause those that have happened earlier.

I think Pearl is successful in his endeavour. I agree with all core theoretical and practical ideas expressed in the book.

Pearl makes a number of speculative propositions (especially at the beginning of the book, about anthropology, and at the end of the book, about AI) which he doesn’t prove, and I disagree with a few of them. But these ideas are peripheral to the central argument of the book.

The structure of the post

I start with the summary of the book’s ideas and arguments, with subsections about causal modelling, interventions, mediation analysis, counterfactuals, causality and big data, causality and ethical AI, and my takeaways from the book. At the end of the post, I present some extra ideas about causality that are not covered nor mentioned in The Book of Why and make some connections between the study of causality and other fields.

Warning: this review is very long, it can take more than an hour to read even if you don’t follow any links. I couldn’t break it up because sections refer to each other.

I think that upon reading this post you should have a good understanding of most of the ideas from The Book of Why. However, I would still recommend reading this book in your leisure time, especially if you like reading about the history of science because this is a well-written and enjoyable book.

---

The summary of the ideas and arguments of The Book of Why

Causal modelling

A causal diagram

A causal diagram (also called a graphical causal model) depicts events, objects, features, characteristics, treatments (all of which are generally called variables in statistics; many synonyms are also used, but I’ll stick to the term “variable” in this post), happening (appearing in, characterising, applying to) in some situation (environment, system). Variables are connected with causal links (arrows) that mean that one variable listens to (caused by) another:

Figure 1. A simple example of a graphical causal diagram with “hidden factor” as a confounder between “smoking” and “lung cancer”.

A causal diagram could be extended with a structural causal model which is described below.

Causal models are subjective

Since the extraction of variables (objects, events, features, etc.) from the background is an operation performed subjectively by an intelligence (an intelligent agent), the causal diagrams are necessarily subjective, too.

Where causation is concerned, a grain of wise subjectivity tells us more about the real world than any amount of objectivity.

While causal diagrams are subjective, statistics are (mostly) objective. Bayesian statistics is the only branch of statistics that also allows for subjectivity (prior beliefs are subjective). However, in Bayesian statistics, as the amount of data (observations) grows, the contribution of prior beliefs vanishes, and the credences become essentially objective. On the other hand, the subjective component in causal information does not diminish as the amount of data increases.

Pearl writes that finding the causal relationships between variables is a scientific process, and, in fact, constitutes a major part of science. Although Pearl doesn’t make this deduction explicitly in the book, this must mean that he thinks that science itself is subjective. I personally agree with this view, but it’s interesting to note that it doesn’t match with the view of David Deutsch, a scientific realist. Deutsch poses that objective, or “most fundamental” causes and effects do exist:

Hofstadter argues that emergent entities (such as people) and abstract concepts (such as numbers, and meanings) really do have causal effects on the microscopic constituents of events. He imagines a computer made of toppling dominoes that is designed to factorize integers. It is presented with the input “641” and set in motion to perform its computation. Why is one particular domino left standing? The most fundamental explanation does not refer to the sequence in which the other dominoes fell; rather it is “because 641 is prime”.

I see no escape from this argument: regarding microphysical explanations as more fundamental than emergent ones is arbitrary and fallacious. [...]

On the other hand, Pearl and Deutsch agree on another aspect of the philosophy of science: they are both constructivists. See the section “Causality is not reducible to probabilities” below.

A Structural Causal Model

A structural causal model (SCM) is a set of equations that corresponds to some causal diagram, where every variable is equated to (i. e., modelled as) a function of its direct causes and an extra random variable for modelling factors that are absent from the diagram, either because they are unknown, intentionally omitted, or unobservable. Each function has its “own” extra random variable, and these random variables are independent of each other. For example, the set of equations corresponding to Figure 1 may look like this:

X = f_X(hidden factor, U_X)

Z = f_Z(X, U_Z)

Y = f_Y(Z, hidden factor, U_Y)

Any functions can be used, including non-analytical. For example, the function could be piece-wise, or the entire form of the function might depend on one of its discrete-valued arguments. Of course, artificial neural networks could be used as these functions, too. If some variable doesn’t need an extra random factor, the latter could be omitted (or a constant random variable used).

When modelling time-series (dynamic processes), the function of each variable value X_i also accepts as an argument its value in the previous moment [1]: X_i = f_X(X_{i-1}, ..., U_X).

How well a structural causal model fits the observational or experimental data is, of course, one of the factors in judging whether the causal model accurately represents reality. The other factor is how generalisable is the model in response to interventions, discussed below in the section ”Interventions are possible because causal mechanisms are assumed to be independent”.

Fully specified structural causal models encode more information about the system than bare causal diagrams: they specify more concretely how variables depend on each other and, possibly, the distributions of the extra random variables. However, a causal diagram can be useful (allows to answer certain questions) even without an accompanying structural causal model.

A structural causal model also embeds implicit or explicit assumptions about the kinds of interventions that are allowed in the model [2].

Interventions: the |do(X) operator and the causal effect

One of the two main types of questions that researchers could ask about the causal model of some situations is a so-called interventional query.

Some examples of interventional queries:

• “How the probability of having a heart attack in the next five years will change in so-and-so group of people if we prescribe them taking so-and-so medicine every day?”

• “How much the sales of a product will change if we discount it by 20%?”

Pearl introduces do-notation for the post-intervention probability distribution, P(Y|do(X)) (or P(Y|do(X = x))) for expressing interventions and distinguishing them from classical conditional probability distributions, P(Y|X). The latter could be biased (more on this below). Unbiased probability distribution equals thes post-intervention probability distribution and its difference with the prior probability distribution (P(Y|do(X)) - P(Y)) is one of the measures of the strength of the (total) causal effect between variables X and Y (sometimes, the ratio P(Y|do(X))/P(Y) is more appropriate). The act of computing or estimating the strength of the causal effect between two variables is called causal inference.

Before Pearl, statisticians didn’t use any special notation to identify unbiased correlation (i. e., the strength of the causal effect). This might seem like a mere relabelling of things until one considers situations in which the correlation can’t be unbiased in a “traditional” sense (by controlling for confounders) but P(Y|do(X)) could nevertheless be estimated: see the section “Front-door adjustment” below.

The graphical interpretation of interventional queries (in fact, Pearl treats this “interpretation” first-class, almost as the definition of interventional queries, and do-notation more like “mathematical interpretation” of them) is erasing the causal links going into X (Pearl metaphorically calls this process “making a surgery”) and setting the value of variable X to a particular value of interest (e. g., a treatment, or a price of a product), or computing a regression, i. e., the strength of the causal effect of X on some other variable, which is equivalent to setting X to multiple different values and seeing how the effect variable responds to this. For the structural causal model, the corresponding surgery is replacing f_X with a constant (X = x) or a single random variable term: X = U_X' (prime distinguishes this variable from U_X which was the argument of the original function f_X).

Generally, an arbitrary non-trivial change of f_X in the structural causal model counts is a valid intervention. An example of a query that demands this advanced type of intervention could be “How much the sales of the product will change if we change the algorithm for computing and setting discounts in such and such way?”

The second important type of causal question is a counterfactual query, which I cover below in this review.

Causality is not reducible to probabilities

Causality can be "defined" as P(Y|do(X)) != P(Y) but this is a tautology of the causal link on the causal diagram, given that |do(X) operator "surgeons" the causal model.

[...] philosophers have tried to define causation in terms of probability, using the notion of “probability raising”: X causes Y if X raises the probability of Y. [...] What prevented the attempts from succeeding was not the idea itself but the way it was articulated formally. Almost without exception, philosophers expressed the sentence “X raises the probability of Y” using conditional probabilities and wrote P(Y | X) > P(Y). This interpretation is wrong, as you surely noticed, because “raises” is a causal concept, connoting a causal influence of X over Y. The expression P(Y | X) > P(Y), on the other hand, speaks only about observations and means: “If we see X, then the probability of Y increases.” But this increase may come about for other reasons, including Y being a cause of X or some other variable (Z) being the cause of both of them. That’s the catch! It puts the philosophers back at square one, trying to eliminate those “other reasons.”

[...] Any attempt to “define” causation in terms of seemingly simpler, first-rung concepts [probabilities and correlations] must fail. That is why I have not attempted to define causation anywhere in this book: definitions demand reduction, and reduction demands going to a lower rung. Instead, I have pursued the ultimately more constructive program of explaining how to answer causal queries and what information is needed to answer them. If this seems odd, consider that mathematicians take exactly the same approach to Euclidean geometry. Nowhere in a geometry book will you find a definition of the terms “point” and “line.” Yet we can answer any and all queries about them on the basis of Euclid’s axioms (or even better, the various modern versions of Euclid’s axioms).

As one can see, Pearl completely sidesteps the questions of the physics (or metaphysics) of causality in the book, instead, he takes a constructivist view on it, which is similar to David Deutsch’s metaepistemology (see a Wikipedia entry on explanatory power): the fact that causality is a powerful concept which allows asking new kinds of questions, answering them, and making predictions that are not possible without this concept is a sufficient reason to use it. See more on this below, in the section “Abstractions have power”.

If one thinks that defining causality is “easy”, for example, as “X causes Y means Y would not happen if not X”, they probably think about so-called necessary (and sufficient) causes. But on a closer look, one notices that both are just sub-categories of contributory/”general” causes (e. g., a necessary cause: P(Y|do(X)) != 0, P(Y|do(~X)) = 0), and this general concept of a cause is still left unexplained. So rest assured that Pearl doesn’t miss something obvious here. And, in fact, he discusses necessary and sufficient causes in the context of counterfactuals.

Causal modelling first, experiment (or study) and data mining second

Pearl describes how researchers should extract knowledge from data: specifically, they should start with creating and analysing a graphical causal model before manipulating the study (or experimental) data. Moreover, researchers should ideally analyse the causal model before even conducting an experiment or an observational study because the causal model could help them to design a better study (experiment), or reveal that their research question is unanswerable, no matter how much data they collect, or that they don’t need any additional data because they can answer their question by “transporting” (translating) information from a combination of earlier studies or experiments, none of which was done in exactly the same context as is of current interest.

Scott Alexander has recently written a post on a related topic: The Phrase "No Evidence" Is A Red Flag For Bad Science Communication.

By providing numerous real-life examples, Pearl proves that data mining and statistics alone are not sufficient to find out whether this or that medicine (treatment), education program, advertising program, and other similar things are effective and to compute the strength of the causal effect (e. g., to compare it with the effects of other treatments or programs).

In certain circles there is an almost religious faith that we can find the answers to these questions in the data itself, if only we are sufficiently clever at data mining. However, readers of this book will know that this hype is likely to be misguided. The questions I have just asked are all causal, and causal questions can never be answered from data alone. They require us to formulate a model of the process that generates the data, or at least some aspects of that process. Anytime you see a paper or a study that analyzes the data in a model-free way, you can be certain that the output of the study will merely summarize, and perhaps transform, but not interpret the data.

The combination of knowledge of correlations with knowledge of causal relations to obtain certain results is a different thing from the deduction of causal relations from the correlations. (Sewall Wright)

Although I agree with this argument in principle, I think the phrases in which Pearl expresses it are vague and could be confusing. I discuss this in the section “Causal relationships could be induced from the data” below.

To find the causal effect between two variables, use controlling judiciously, informed by the causal model

The correlation between the treatment (program) and the effect may vary greatly, or even disappear and then reappear again, depending on the set of controlling variables.

An attempt to “play it safe” and to control for every observable variable (except the treatment and the effect variables) to eliminate all conceivable confounding biases isn’t always correct because controlling for a collider variable opens a parasitic information flow between the colliding variables. This is called a “collider bias”.

The author gives a fascinating example of the collider bias: it appears in the famous Monty Hall paradox. It paradoxically appears that the original choice of the door by the player is (negatively) correlated with the door behind which there is the car (and this is why the player needs to change their original choice after the host opens another door), which seems like the original choice of the door affects the location of the car because the door opened by the host is the causal collider of the player’s door of choice and the door behind which there is a car:

The player becoming aware of the door opened by the host is an act of conditioning on this variable which leads to a collider bias as well as controlling.

Besides, to find answers to interventional queries P(Y|do(X)), controlling for a lot of variables is often unnecessary, and while it formally should lead to the correct result, it could be challenging to do this and to preserve the accuracy and the precision of the analysis because of the curse of dimensionality.

There can be a correlation without a causation

The Monty Hall paradox is a counterexample to the Reichenbach’s Common Cause Principle: “If two variables X and Y are statistically dependent, then there exists a variable Z that causally influences both and explains all the dependence in the sense of making them independent when conditioned on Z.” However, as one can see, door chosen by the player originally and car location are statistically dependent but don’t have a common cause.

I would add that in some cases, correlations are purely random coincidences. Even a fair coin could land fails one hundred times in a row. The tsunami of big data, as Nassim Taleb warns, implies that overzealous researchers can find more and more such correlations in the real world:

© Tyler Vigen

The way the data is collected can introduce bias

Aaron Roth and Michael Kearns write in The Ethical Algorithm that researchers shouldn’t access data too much before forming a hypothesis because they can p-hack without intending to. The mechanism of this bias could be the same as in the Monty Hall paradox: if the way the data is collected (i. e., the design of the study) is affected by both the cause and the effect variables, then an additional correlation path is opened between these variables.

Even the decision to stop the study at some point upon seeing a strong correlation (confirming researchers’ hypothesis) is a part of the design of the study and thus might introduce bias.

Back-door criterion

Researchers should look at the causal diagram to determine whether there is a set of variables for which the observational or experimental data could be controlled to obtain the causal effects between the treatment and the effect (in other words, whether it is possible to compute the causal effect at all). The blocking variables (i. e., the variables for which researchers should control their data) should block all so-called back-door paths (detailed explanation of what does this mean is beyond the scope of this review) between variables X and Y while not blocking any front-door paths (i. e., the paths consisting only of forward causal arrows) between X and Y. A set of such variables is said to satisfy the back-door criterion.

If researchers can identify a minimal set of such blocking variables that are all observable and for which they have data, they can compute the causal effect between X and Y by controlling only for these variables, and none more. If there is no such set, then the causal effect cannot be estimated, no matter how much data is collected (this situation is discussed further in the section “How does causal modelling relate to the study of complex systems” below).

Sometimes, the set of blocking variables is empty, which should be taken as proof that the post-interventional probability equals simple conditional probability (P(Y|do(X) = (Y|X)) and can be used to compute the causal effect between X and Y without any further adjustment.

Pearl suggests several ways of dealing with the situation when every minimal set of blocking variables includes at least one unobservable variable or one which is absent in the available study or experimental data:

• Find ways to obtain the data on these variable(s), which can range from conducting an additional survey among the patients to developing new scientific knowledge or technology for measuring or estimating the variables that were unobservable before, for example, activity of neurons in the brains of people in casual settings for neuroscience and psychology research.

• Make simplifying assumptions (at the risk of being wrong): for example, that an effect of one variable on another is small and can be neglected. If researchers choose this path, ideally, they should supplement their results with a sensitivity analysis (more on this below).

• Use front-door adjustment instead, if applicable (more on it below).

In research, make assumptions liberally and then discard implausible ones

Instead of drawing inferences by assuming the absence of certain causal relationships in the model, the analyst challenges such assumptions and evaluates how strong alternative relationships must be in order to explain the observed data. The quantitative result is then submitted to a judgment of plausibility, not unlike the crude judgments invoked in positing the absence of those causal relationships.

Pearl doesn’t mention that this proposition about how causal discovery should be done is a special case of Karl Popper’s “bold hypothesis” idea:

... there is no more rational procedure than the method of trial and error – of conjecture and refutation: of boldly proposing theories; of trying our best to show that these are erroneous; and of accepting them tentatively if our critical efforts are unsuccessful. From the point of view here developed, all laws, all theories, remain essentially tentative, or conjectural, or hypothetical, even when we feel unable to doubt them any longer.

Researchers can find causal mechanisms in data from observational studies as well as from controlled experiments

Pearl suggests researchers should be bolder in their claims, which is related to the previous idea of “bold hypothesis”:

Researchers have been taught to believe that an observational study (one where subjects choose their own treatment) can never illuminate a causal claim. I assert that this caution is overexaggerated. Why else would one bother adjusting for all these confounders, if not to get rid of the spurious part of the association and thereby get a better view of the causal part?

Instead of saying “Of course we can’t,” as they did, we should proclaim that of course we can say something about an intentional intervention. If we believe that Abbott’s team identified all the important confounders, we must also believe that intentional walking tends to prolong life (at least in Japanese males).

This provisional conclusion, predicated on the assumption that no other confounders could play a major role in the relationships found, is an extremely valuable piece of information. It tells a potential walker precisely what kind of uncertainty remains in taking the claim at face value. It tells him that the remaining uncertainty is not higher than the possibility that additional confounders exist that were not taken into account. It is also valuable as a guide to future studies, which should focus on those other factors (if they exist), not the ones neutralized in the current study. In short, knowing the set of assumptions that stand behind a given conclusion is not less valuable than attempting to circumvent those assumptions with an RCT (randomised controlled trial), which, as we shall see, has complications of its own.

Front-door adjustment

Pearl presents the method called front-door adjustment for estimating the causal effect of one variable on another when these variables have unknown or unobserved confounders which makes it impossible to estimate the causal effect the “traditional way”, by controlling for confounders. The method is also applicable only in special situations (there should be an unconfounded and observable mediator variable on the causal path between the treatment and the effect variables), but the point is that it is impossible to demonstrate why the front-door adjustment is a valid method without reaching to the notions of causality and causal mediation.

Note that statistical methods such as linear regression are used to estimate the total effect of X on Y (P(Y|do(X))), both with controlling and front-door adjustment formula, even, as was noted above, it’s not possible to judge whether the result indeed represents the unbiased causal effect of X on Y (and what variables should be controlled for) without also using a causal model or making causal assumptions.

Mediation analysis

Only after a researcher uses the notions of cause and effect, they can ask whether a treatment causes an effect directly or indirectly, that is, mediated through the effect of the treatment variable on other variables different from the effect variable. This, in turn, will help a researcher to refine their causal model, thus beginning a virtuous loop of discovery of causal relationships. Pearl poses that these relationships constitute the bulk of the whole scientific knowledge, as noted in the section "Causal models are stored in human minds in reference frames” below.

Baron & Kenny’s approach to mediation analysis

Baron and Kenny developed a famous procedure for mediation analysis using multiple regression over variables X (cause), Y (effect), and the mediating variable M (the procedure could be straightforwardly generalised for the situations with multiple mediators). Baron & Kenny essentially defined the regression of Y on X controlled for M as direct effect, and posit that total effect = direct effect + indirect effect. Note the absence of the word “causal” in these labels. Pearl writes that Baron & Kenny’s method estimates noncausal mediation (The Book of Why, p. 325), despite David Kenny himself stating the exact opposite on his website:

Note that a mediational model is a causal model. For example, the mediator is presumed to cause the outcome and not vice versa. If the presumed causal model is not correct, the results from the mediational analysis are likely of little value. Mediation is not defined statistically; rather statistics can be used to evaluate a presumed mediational model.

I agree with Pearl, though, that Baron & Kenny’s definition of direct effect and indirect effect is purely mathematical. Pearl points this in [3], on page 3 (note: variable name “Z” is replaced with “M” in this quote for consistency with the rest of this page):

Remarkably, the regressional estimates of the difference-in-coefficients and the product-of-coefficients will always be equal. This follows from the fact that the regressional image of (1), R_YX − R_YX·M = R_MX*R_YM·X, is a universal identity among regression coefficients of any three variables, and has nothing to do with causation or mediation. It will continue to hold regardless of whether confounders are present, whether the underlying model is linear or nonlinear, or whether the arrows in the model of Fig. 1(a) point in the right direction.

Pearl shows that this procedure only has meaning when the causal relationships underlying the observations are linear, that is, in a structural causal model for the system, f_M(X, U_M) and f_Y(X, M, U_Y) can be modelled as linear functions. If the causal relationships between variables are non-linear, the numerical values for direct effect and indirect effect produced by following Baron & Kenny’s procedure cannot be associated with some discernible real-world quantity, i. e., don’t have a meaning.

I’ll explain this and will discuss the implication in the sections following the next one after I present Pearl’s approach to mediation analysis:

Pearl’s measures for mediation analysis: natural direct and indirect effects

For mediation analysis, Pearl suggested using notions of natural direct effect (NDE) and natural indirect effect (NIE) which are defined as follows:

The natural direct effect of the transition from X = x to X = x’ is the expected change in Y induced by changing X from x to x’ while keeping M constant at whatever value they would have obtained (for a specific situation/system/individual) under X = x, before the transition from x to x’.

Mathematically, in terms of a structural causal model,

NDE(X = x → X = x’) = E[f_Y(x’, f_M(x, u_M), u_Y)] − E[f_Y(x, f_M(x, u_M), u_Y)],

Where u_M and u_Y are some particular values that the extra random variables U_M and U_Y assume in the specific situation (instance of the system, individual patient, etc.).

The natural indirect effect of the transition from X = x to X = x’ is the expected change in Y affected by holding X constant, at X = x, and changing M to whatever value it would have attained had X been set to X = x’ (for a specific situation/system/individual).

Mathematically, in terms of a structural causal model,

NIE(X = x → X = x’) = E[f_Y(x, f_M(x’, u_M), u_Y)] − E[f_Y(x, f_M(x, u_M), u_Y)],

The only difference of which from the expression for NDE(X = x → X = x’) is the switch of x and x’ in the first half of the expression.

If we also define total causal effect (TE) in terms of SCM as

TE(X = x → X = x’) = E[f_Y(x', f_M(x’, u_M), u_Y)] − E[f_Y(x, f_M(x, u_M), u_Y)],

it’s easy to notice that TE(X = x → X = x’) != NDE(X = x → X = x’) + NIE(X = x → X = x’), which might seem surprising, but is internally consistent, unlike Baron & Kenny’s definitions of direct and indirect effect, which “must” add up to the total effect. An alternative equation holds:

TE(X = x → X = x’) = NDE(X = x → X = x’) - NIE(X = x’ → X = x): the total causal effect equals the natural direct effect of the transition from X = x to X = x’ minus the natural indirect effect of the transition from X = x’ to X = x (note the reverse direction).

It’s also crucial that natural direct effect and natural indirect effect are defined for specific situations (instances of system, individuals, etc.), which means they are counterfactual notions (discussed in a corresponding section below).

Therefore, average natural direct effect and average natural indirect effect, unlike total causal effect, cannot be computed with a single-step regression (as in Baron & Kenny’s procedure), but only with two-step regression, essentially integrating over all possible values of x (of variable X) and m (of variable M) that appear in the data set. The curse of dimensionality may preclude a researcher from doing non-parametric regressions. In this case, they should use parametric approximations, which means they must assume a hypothesis about the shape of f_M and f_Y functions in the structural causal model if they haven’t done this before. The details are in [3] (but not in The Book of Why).

Detailed analysis of Pearl’s arguments against Baron & Kenny’s approach

Pearl uses various vague and metaphorical phrases to express his opinion of Baron & Kenny’s approach. I italicised these characteristic phrases in the quotes below.

The Book of Why, p. 325:

However, cracks in this regression-based edifice began to appear in the early 2000s, when practitioners tried to generalize the sum-of-products rule to nonlinear systems. That rule involves two assumptions—effects along distinct paths are additive, and path coefficients along one path multiply—and both of them lead to wrong answers in nonlinear models, as we will see below. It has taken a long time, but the practitioners of mediation analysis have finally woken up.

It’s important to note here that later, Pearl doesn’t show how Baron & Kenny’s approach leads to “wrong answers” which would at least require specifying the questions, which Pearl actually doesn’t do in the text following this quote. The strongest condemnation that appears on the next page refers to “unnaturalness” and “more intuitive sense”:

If we want to preserve the additive principle, Total Effect = Direct Effect + Indirect Effect, we need to use CDE(2) as our definition of the causal effect. But this seems arbitrary and even somewhat unnatural. If we are contemplating a change in Education and we want to know its direct effect, we would most likely want to keep Skill at the level it already has. In other words, it makes more intuitive sense to use CDE(0) as our direct effect. Not only that, this agrees with the natural direct effect in this example. But then we lose additivity: Total Effect ≠ Direct Effect + Indirect Effect.

However, the problem with this pronouncement of the inconsistency of Baron & Kenny’s approach to a situation where one of the functions in the structural causal model is non-linear is recursive, because structural causal modelling with non-linear equations is wholly a part of Pearl’s framework of causal reasoning, not Baron & Kenny’s. This is similar to proving that some theorem, derived from one set of assumptions, is “wrong” given some different assumptions.

The Book of Why, p. 328:

Both groups of researchers confused the procedure with the meaning. The procedure is mathematical; the meaning is causal. In fact, the problem goes even deeper: the indirect effect never had a meaning for regression analysts outside the bubble of linear models. The indirect effect’s only meaning was as the outcome of an algebraic procedure (“multiply the path coefficients”). Once that procedure was taken away from them, they were cast adrift, like a boat without an anchor.

I agree with Pearl here that Baron & Kenny’s direct and indirect effect values don’t have meaning while Pearl’s natural direct and indirect effects do, if we take “meaning” in the sense that Douglas Hofstadter ascribed to this word in Gödel, Echer, Bach, that is, something that is implied by an isomorphism between symbols: in our case, terms “direct effect” and “indirect effect”, and some objects in another system: in our case, quantities in the real world and imaginary worlds (the latter are also real in the Everettian universe). In the previous section, I’ve given Pearl’s definitions for natural direct and indirect effects that specifically point to the quantities in the world. No such correspondence exists for Baron & Kenny’s direct and indirect effects.

Yet, despite this absence of meaning behind Baron & Kenny’s notions of direct and indirect effects is a strong argument for using Pearl’s notions of natural direct and indirect effects, it’s not a logically decisive argument for doing so for all purposes. I could imagine a situation (though cannot come up with a real example), when, despite having some real-world objects or quantities to point at (i. e., the meaning), some measures don’t match well the human intuition behind some terms, due to the language semantics. Therefore, such measures would not aid human understanding. See the section “Could mediation analysis help refine humans’ intuitive causal models of phenomena?” below for more detailed discussion.

[3], p. 3:

As a consequence, additions and multiplications are not self-evident in nonlinear systems. It may not be appropriate, for example, to define the indirect effect in terms of the “difference” in the total effect, with and without control. Nor would it be appropriate to multiply the effect of X on Z by that of Z on Y (keeping X at some level) – multiplicative compositions demand their justifications. Indeed, all attempts to define mediation by generalizing the difference and product strategies to nonlinear system have resulted in distorted and irreconcilable results.

The occasional usage of stronger language, such as in phrases “lead to wrong answers” and “irreconcilable results”, have led me to a belief that there should be something mathematically wrong with Baron & Kenny’s approach in the transition between linear causal mechanisms (for which Pearl’s and Baron & Kenny’s approaches lead to mathematically identical expressions of direct and indirect effects) and non-linear mechanisms. I thought that this proof might stem somehow from Jensen’s inequality and looked for references in Pearl’s papers. Finally, I realised that there are no such mathematical problems with Baron & Kenny’s approach, which Pearl highlighted himself in [3]:

Remarkably, the regressional estimates of the difference-in-coefficients and the product-of-coefficients will always be equal. This follows from the fact that the regressional image of (1), R_YX − R_YX·Z = R_ZX*R_YZ·X, is a universal identity among regression coefficients of any three variables, and has nothing to do with causation or mediation. It will continue to hold regardless of whether confounders are present, whether the underlying model is linear or nonlinear, or whether the arrows in the model of Fig. 1(a) point in the right direction.

Pearl writes that Baron & Kenny’s approach “has nothing to do with causation or mediation”, and his argument is “[Baron & Kenny’s equation] will continue to hold regardless of whether confounders are present, whether the underlying model is linear or nonlinear, or whether the arrows in the model of Fig. 1(a) point in the right direction.” But I think this conclusion is premature. This argument merely shows that Baron & Kenny’s procedure is not a reliable method for determining whether there is mediation. David Kenny recognises this in [4]:

[...] the mediator is presumed to cause the outcome and not vice versa. If the presumed causal model is not correct, the results from the mediational analysis are likely of little value.

Kenny suggests that researchers should perform additional sensitivity analyses.

Let’s assume there are no confounders between X, M, and Y (except that X is the confounder for M and Y), and all causal links point in the correct directions. Then I don’t see any ground for Pearl’s claim “[Baron & Kenny’s equation] has nothing to do with causation or mediation”, except that in some cases it leads to less intuitive values for direct and indirect effects than Pearl’s natural direct and indirect effects (NDE and NIE).

Inconsistency of Kenny’s prepositions

In fairness, here I play the role of Kenny’s advocate because in [4] his prepositions are sometimes inconsistent with each other. For example, he writes that their (with Reuben Baron) procedure is the “steps in establishing mediation”, which is hard to interpret in any other way than that these steps can be used to determine whether there is mediation (they can not, as noted above). But just on the previous line, he writes “We note that these steps are at best a starting point in a mediational analysis.”

In the “Introduction” in [4], he starts with pictures of causal diagrams (models) and writes that some path on a model is called “direct effect”. This means that he assumes direct effect to be a part of the model. In the next paragraph, he seemingly contrasts causal (mediational) modelling and mediational analysis (which is confusing in itself):

Note that a mediational model is a causal model. For example, the mediator is presumed to cause the outcome and not vice versa. If the presumed causal model is not correct, the results from the mediational analysis are likely of little value. Mediation is not defined statistically; rather statistics can be used to evaluate a presumed mediational model.

But then, as I already noted above, he defined direct effect as a regression coefficient, which places it into mediational analysis(?) and not mediational modelling.

Two goals of mediation analysis

To better understand the difference between Baron & Kenny’s and Pearl’s methods for mediation analysis, I think it’s essential to start with the purpose: why researchers perform mediation analysis in the first place?

I think it’s reasonable to point out two big goals. One goal is answering concrete counterfactual questions in service of planning and decision making. This counterfactual query answering module could also be embedded within a larger machine or hybrid intelligence architecture. Another goal is helping humans to understand the causal model of some process (system, situation, etc.) better.

Compute natural direct effect to answer questions and improve decisions

For the first goal, Pearl gives examples of such concrete, practical counterfactual questions. In American court, discrimination is taken to mean natural direct effect:

The central question in any employment-discrimination case is whether the employer would have taken the same action had the employee been of a different race (age, sex, religion, national origin, etc.) and everything else had been the same.

Other similar questions may arise in medication development: if a drug had a different composition, how effective would it be, given its mediation factors?

It’s indisputable that natural direct effect (and, perhaps, sometimes, natural indirect effect) should be used to help answer questions like these and guide decisions.

Could mediation analysis help refine humans’ intuitive causal models of phenomena?

Apart from the “computational” (instrumental) purpose described above, mediation analysis is also supposed to have another function: help communicate “computed” decisions to humans, as part of the explainable AI program.

As I noted above, Pearl’s natural direct effect and natural indirect effect have a huge advantage over Baron & Kenny’s direct and indirect effects because they can be associated with some concrete quantities in the real world. However, NDE and NIE also have a huge disadvantage: humans’ intuition about language strongly suggests that direct and indirect effects should add up to 100% (i. e., the total effect), but they don’t. Baron & Kenny’s measures are specifically designed to always add up to 100%, which is their advantage.

I considered if rebranding natural indirect effect into something like “mediated effect” would help to overcome this problem with Pearl’s measures. However, it’s not just the names that are counter-intuitive. Pearl himself gives an example in the book when both NDE and NIE of treatment are equal to zero, which would not help people to hone their mental models of how the treatment works, regardless of the label given to NIE. In that case, the total effect of treatment is equal to the negated natural indirect effect of cancelling the treatment. Needless to say that this convoluted, “mathematical” phrase could hardly improve anyone’s intuitive understanding, either.

I came to the conclusion that for the purposes of human communication, Pearl’s measures are not always compressible to term equations like NDE = a and NIE = b, but should rather be conveyed through examples (full counterfactual statements), such as “both medicine (the treatment) and enzyme (the mediator) don’t help to improve patient’s condition (the effect) at all”.

Counterfactuals

The second main type of causal inference question is counterfactual (the first type was interventional queries).

Some examples of counterfactual queries, corresponding to the examples of interventional queries that were given above:

• “Given that the patient has had a heart attack, what is the probability that they wouldn’t have a heart attack if he started to take so-and-so medicine one year ago?”

• “Given that the customer didn’t buy the product, what is the probability that he would if he was offered a 20% discount?”

Interventional queries are about aggregates and distributions, counterfactual queries are about specific instances and samples in the distributions

The terms “interventional query” and “counterfactual query” might suggest that the difference between them is that interventional questions are concerned with the future, while counterfactual questions are concerned with the past, even if the “past” in some imaginary world, which itself might be in the “future” (counter-fact, i. e. something against what have happened in fact). This is wrong and caused a lot of confusion for me while I was reading the book.

The actual difference between interventional and counterfactual queries is following:

Interventional queries are about groups of units, and therefore don’t need to sample from the U_X, U_Y, etc. extra random variables in the structural causal model. Actually, this allows answering interventional queries such as P(Y|do(X)) without having a structural causal model at all, but only a causal diagram, as described above in the sections about controlling, back-door criterion, and front-door adjustment.

Counterfactual queries are about a specific unit (patient, situation, instance of the system), and rely on the concrete u_x, u_y, etc. values for the extra random variables in the structural causal model. That’s why counterfactual queries are not answerable without at least a partially specified SCM. For typical SCMs, the values assumed by the random variables are unknown for the situation as it will unfold in the future, which is the reason why counterfactual queries are almost always asked about the past.

Therefore, a question like “We sold X units of the product in the last quarter. How many would we sell if we reduced the price by 20%?” is an interventional question, despite it is concerned with the past. This holds true if the causal model against which the question is asked has variables such as “a customer”, “an impression”, “the need for product”, “a purchase”, i. e., the model in which the question is about the gross number of purchases. If exactly the same question was asked against the model where “product”, “market demand”, “market supply”, “total number of customer impressions”, etc. were individual variables, this would be a counterfactual question, because the question would be about the single unit (the product) in that model.

Conversely, the question “What is the probability that this specific patient wouldn’t have a stroke in the next 5 years if he started to take so-and-so medicine daily, starting today?” is a counterfactual question (despite it’s not “counter” any fact, and is purely about the future) if the causal model against which this question is asked has “patient”, “medication”, and “a stroke” as its variables. However, this question couldn’t be answered because of the random factors that are not even specified in the model and are unknowable: for example, what if the patient will be stressed a lot due to something that will happen to him a year from now? When people try to answer such questions, they implicitly convert them into populational, i. e. interventional questions: “what is the probability that a person with exactly the characteristics that the given patient has: age, weight, genetic disposition, accompanying illnesses, etc. wouldn’t have a stroke in the next 5 years if they started to take so-and-so medicine daily?”, or, mathematically, P(stroke|do(age, weight, genetic disposition, accompanying illnesses)).

Notation for counterfactual queries

In the book, Pearl introduces separate notation for counterfactual queries but doesn’t follow it strictly, sometimes he just uses do-notation to represent counterfactual queries (as well as the authors of [2]). In do-notation, counterfactual queries can be written as P(Y|u, do(X = x)) where u abbreviates all specific values u_x, u_y, etc. assumed by random variables U_X, U_Y, etc. for the concrete unit in the question.

“The Ladder of Causation”

Pearl organises simple statistical queries, P(Y|X), interventional queries, P(Y|do(X)), and counterfactual queries, P(Y|u, do(X = x)) into what he calls “The Ladder of Causation”.

Pearl associates words “imagining”, “retrospection”, and “understanding” with counterfactual reasoning (”the top-rung of the ladder of causation” as he calls it). This seems confusing to me: I don’t understand why interventional queries are not about “imagining” (any more than counterfactual queries, at least—since answering both, in the end, boils down to performing mathematical operations with certain models and data according to certain rules). Answering interventional queries (and especially performing sensitivity analysis) can also help to improve the causal models, so they help to build a scientific understanding of phenomena as well as counterfactual queries in the course of mediation analysis. And I’m not even talking about building an intuitive human understanding of how the causal model works, which is surely improved by answering a series of interventional queries.

For these reasons, putting interventions below counterfactuals on the “Ladder” seems somewhat arbitrary to me.

Humans are the only animals capable of counterfactual reasoning

Pearl also attaches to “The Ladder of Causation” some anthropological and biological propositions, such as that among animals, only humans are capable of counterfactual reasoning.

David Graeber and David Wengrow cite Cristofer Boehm in The Dawn of Everything for suggesting exactly this:

[...] while gorillas do not mock each other for beating their chests, humans do so regularly. Even more strikingly, while the bullying behaviour might well be instinctual, counter-bullying is not: it’s a well-thought-out strategy, and forager societies who engage in it display what Boehm calls ‘actuarial intelligence’. That’s to say, they understand what their society might look like if they did things differently: if, for instance, skilled hunters were not systematically belittled, or if elephant meat was not portioned out to the group by someone chosen at random (as opposed to the person who actually killed the beast). This, he concludes, is the essence of politics: the ability to reflect consciously on different directions one’s society could take, and to make explicit arguments why it should take one path rather than another. In this sense, one could say Aristotle was right when he described human beings as ‘political animals’ – since this is precisely what other primates never do, at least not to our knowledge.

On the other hand, Pearl mentions in his book the “Cognitive Revolution”, the idea that Graeber and Wengrow debunk in their book.

Human intuition is “organised around causal relationships”?

The knowledge conveyed in a casual diagram is typically much more robust than that encoded in a probability distribution. This is the reason, Pearl conjectures, that human intuition is organised around casual, not statistical relations.

The classic story that is typically invoked to substantiate this idea is about toddlers already capable of inferring causal relationships between events. I didn’t really review the literature on this subject, but it seems to me that “events” in the question are invariably physical and what toddlers can see, such as balls moving, toys changing, etc.

I agree that human intuition about physical and seeable events is “causal” (and even this intuition is probably limited to physical events governed by classical mechanics, and doesn’t extend to electromagnetism). However, it doesn’t seem proven to me that human intuition about abstract events (such as actions taken by corporations, diseases, political events) is causal, too.

Human’s intuitive thinking approximately corresponds to Daniel Kahneman’s “system one”/S1 (see my recent post about this: “Formal reasoning, intuition, and embodied cognition in decision making”), which is statistical, not causal: “What You See Is All There Is” (WYSIATI). A consequence of WYSIATI is that people evaluate events without considering alternatives, which is another way of saying that people don’t think counterfactually intuitively. True counterfactual reasoning requires serious deliberation, “system two”/S2 thinking per Kahneman.

Therefore, I would say that statement “human intuition is organised around causal relationships” is oversimplified and is not correct: the kind of causal relationships matters.

Causality and big data

Causal relationships could be induced from the data

In the section “Causal modelling first, experiment (or study) and data mining second” above, I’ve relayed Pearl’s idea that data mining, statistics, and even deep learning alone (without an assumed causal model) are insufficient to estimate the causal effect between a pair of variables.

In the end, one can say, this statement surely must be false because the totality of (scientific) knowledge has been produced by human brains (albeit across many generations), and, more recently, by computers, using only sensory experiences and “random noise” as inputs. In some broad sense, this whole process was (and continues to be) just data mining, statistics, and deep learning.

Pearl agrees that causal relationships could be induced (hypothesised, discovered) from the data. Machine intelligence could assist in this process or even perform it entirely on its own.

The branch of machine learning that is concerned with learning causal models from data is called causal representation learning [2]. It also often makes sense to learn causal mechanisms together with the causal variables themselves (feature, object extraction) within an integrated intelligence model.

What Pearl really hints at in his “insufficiency” argument is that data mining and standard machine learning methods (i. e., those that don’t embed causality in the structure of the learned model) can compute some relationships between variables, but these results will probably not be robust enough for answering interventional and counterfactual questions.

The role of big data in causal modelling and inference

Pearl suggests the following ways to leverage big data for causal modelling and inference:

• With big data, researchers can search for interesting patterns of association and pose more precise interpretive questions.

• The sheer quantity of data samples helps to overcome the curse of dimensionality in computing certain causal queries. In fields where there is a big variance in symptoms and histories (such as personalised medicine), units (e. g., patients) could be first clustered based on some similarity metric, and then interventional queries answered based on the data samples in the cluster: consider P(stroke|do(age, weight, genetic disposition, accompanying illnesses)) query mentioned in the section “Interventional queries are about aggregates and distributions, counterfactual queries are about specific instances and samples in the distributions” above.

In 2020, Jeffrey Wong published a paper about computational causal inference [5]:

We introduce computational causal inference as an interdisciplinary field across causal inference, algorithms design and numerical computing. The field aims to develop software specializing in causal inference that can analyze massive datasets with a variety of causal effects, in a performant, general, and robust way. The focus on software improves research agility, and enables causal inference to be easily integrated into large engineering systems. In particular, we use computational causal inference to deepen the relationship between causal inference, online experimentation, and algorithmic decision making.

This paper describes the new field, the demand, opportunities for scalability, open challenges, and begins the discussion for how the community can unite to solve challenges for scaling causal inference and decision making.

Pearl didn’t mention, however, the peril of using big data in research: the risk of finding a spurious correlation where there is none, as described in the section “There can be a correlation without a causation” above.

Causality and ethical AI

The role of causal reasoning in understanding free will, consciousness, and agency

Unlike on the subject of anthropology, Pearls makes very cautious statements about the role of causal reasoning in the “holy grail topics of artificial intelligence”, namely free will, consciousness, agency, responsibility, ethics, etc. I think these are all uncontroversial statements:

The illusion of free will gives us the ability to speak about our intents and to subject them to rational thinking, possibly using counterfactual logic.

I believe that the algorithmization of counterfactuals is a major step toward understanding these questions and making consciousness and agency a computational reality.

I believe that the software package that can give a thinking machine the benefits of agency would consist of at least three parts: a causal model of the world; a causal model of its own software, however superficial; and a memory that records how intents in its mind correspond to events in the outside world.

This proposition is based on the following definition of agency that Pearl uses: “the ability to reason about one’s own beliefs, intents, and desires”.

The first requirement of a moral machine is the ability to reflect on its own actions, which falls under counterfactual analysis.

Notably, Pearl looks at consciousness and free will in pretty much the same way as Joscha Bach does (see, for example, this interview). And Joscha Bach is a scientific subjectivist (as well as Pearl, as I infer from the book), unlike David Deutsch and Chiara Marletto (see this discussion between Marletto and Bach).

Asimov’s laws of robotics would not work because lists of rules never work in AI

There is a big difference in spirit between the causal approach to building the moral robot and an approach that has been studied and rehashed over and over in science fiction since the 1950s: Asimov’s laws of robotics. Isaac Asimov proposed three absolute laws, starting with “A robot may not injure a human being or, through inaction, allow a human being to come to harm.” But as science fiction has shown over and over again, Asimov’s laws always lead to contradictions. To AI scientists, this comes as no surprise: rule-based systems never turn out well. But it does not follow that building a moral robot is impossible. It means that the approach cannot be prescriptive and rule based.

Do empathy and fairness follow self-awareness?

Pearl writes:

Once we program self-awareness, however limited, empathy and fairness follow, for it is based on the same computational principles, with another agent added to the equation.

This statement is not proven and looks wrong to me.

Self-awareness doesn’t automatically imply empathy and fairness: sociopaths are self-aware but lack empathy. Fairness is one of the moral foundations (according to the moral foundations theory) and could, in principle, be disregarded even by healthy people (that is, non-sociopaths), at least in the sense that people in the liberal West associate with this word. Jonathan Haidt deals with these questions at length in The Righteous Mind.

Pearl’s views on the risks of AI

[...] we should equip thinking machines with the same cognitive abilities that we have, which include empathy, long-term prediction, and self-restraint, and then allow them to make their own decisions.

Once we have built a moral robot, many apocalyptic visions start to recede into irrelevance. There is no reason to refrain from building machines that are better able to distinguish good from evil than we are, better able to resist temptation, better able to assign guilt and credit. At this point, like chess and Go players, we may even start to learn from our own creation. We will be able to depend on our machines for a clear-eyed and causally sound sense of justice. We will be able to learn how our own free will software works and how it manages to hide its secrets from us. Such a thinking machine would be a wonderful companion for our species and would truly qualify as AI’s first and best gift to humanity.

These are literally the last words of the main content of the book. Pearl doesn’t explain his positions further. Saying that machines can distinguish good from evil “better” than humans implies that Pearl is a moral realist, which is surprising, because, as I noted in the section “Causal models are subjective” above, he seems to me scientific subjectivist, and I would expect people who are scientific subjectivists to be moral subjectivists, too (or constructivists, or hold another similar, non-objective meta-ethical position).

In this interview, Pearl expands his position:

Lex Fridman: Do you have concerns about the future of AI? All the different trajectories of our research?

Judea Pearl: I’m concerned because I know we are building a new species that can exceed our capabilities and can breed itself and can take over the world. Absolutely, it’s a new species, it’s uncontrolled. We don’t know the degree to which we control it, we don’t even understand what it means to be able to control this new species. I don’t have anything to add to this because it’s such a grey area that is unknown. This has never happened in history.

Conclusions and takeaways

I was looking for a book that would introduce me to practical applications of statistics and yet was not very technical, i. e. would not submerge me into the subtleties of specific probability distributions and statistical procedures. The Book of Why is just such a book.

The state-of-the-art of causal modelling within machine intelligence architectures is quickly moving forward and is not reflected in the book.

Below, I point out my main practical takeaways from the book.

Abstractions have power

In The Book of Why, Pearls gives several examples of situations when researchers couldn’t effectively answer certain questions because they didn’t use the language of causality, thinking about causality as a mirage that is reducible to probabilities:

[...] as an expert in occupational health and safety, [Jamie] Robins had been asked to testify in court about the likelihood that chemical exposure in the workplace had caused a worker’s death. He was dismayed to discover that statisticians and epidemiologists had no tools to answer such questions. This was still the era when causal language was taboo in statistics. It was only allowed in the case of a randomized controlled trial, and for ethical reasons one could never conduct such a trial on the effects of exposure to formaldehyde.

In this situation, though, the question (”Has chemical exposure caused a worker’s death?”) was already known, thanks to the fact that causality was already present in the human language and in the philosophical and legal discourse, although statisticians have attempted to deny its existence in the 20th century.

But the true magic happens when a new concept (or a web of concepts, i. e. a new theory) is identified and the agents that use these new abstractions suddenly gain new power, which they didn’t even think was possible before. The paradox of the situation after a paradigm shift, the agents couldn’t understand the myopia of those who don’t use the new theory (language, abstractions) yet (this phenomenon is called metanoia), and the agents in this latter group couldn’t understand what the power even is until they get acquainted with the new theory themselves.

The idea that abstractions have power is not invented by Pearl, of course, but The Book of Why serves as a good reminder.

Stephen Wolfram writes in the article “Logic, Explainability, and the Future of Understanding”:

[…] breakthroughs—whether in science, technology or elsewhere—are very often precisely associated with the realization that some new category or concept can usefully be identified.

Richard Hamming writes in The Art of Doing Science and Engineering:

It has long been recognised the initial definitions determine what you find, much more than most people care to believe. The initial definitions need your careful attention in any new situation, and they are worth reviewing in fields in which you have long worked so you can understand the extent the results are a tautology and not real results at all.

There is the famous story by Eddington about some people who went fishing in the sea with a net. Upon examining the size of the fish they had caught they decided there was a minimum size to the fish in the sea! Their conclusion arose from the tool used and not from reality.

Make a causal model of an important system you are dealing with

Examples of such systems are your own motivation (mood, health, quality of sleep, etc.), an organisation you are leading, or a system you are building.

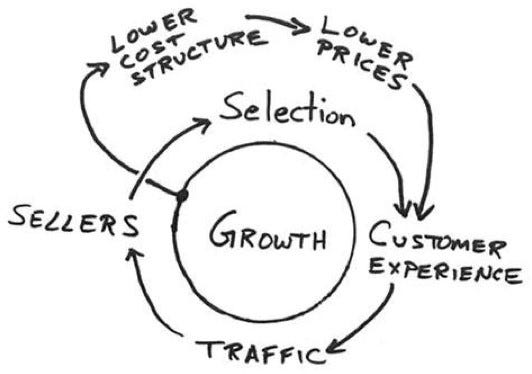
The famous “Amazon Flywheel” which Jeff Bezos drew is such a causal diagram:

The Amazon’s Flywheel.

In Working Backwards (a book about Amazon’s culture), Colin Bryar and Bill Carr recommend thinking about the implications of this causal diagram for the organisational structure, the culture, and the strategy of the organisation.

A causal diagram of a system can be considered one of the types of system views. A causal diagram can be less formal than a data flow diagram or a money flow diagram or even a “value” flow diagram, as one can see in the example of “Amazon’s flywheel” (see above). But covering this informal, intuitive spectrum of thinking about systems might is as important as more formal thinking. I wrote about this in a recent post about intuitive thinking in business and engineering.

The Amazon’s flywheel looks more like a system archetype (from the study of system dynamics; see also the section “How does causal modelling relate to the study of complex systems” below) than any causal diagram from The Book of Why (they are all directed acyclic graphs). This is accidental. I think the diagrams of system dynamics are overly focused on the endogenous factors and don’t pay enough attention to external influences on the system and the priors.

Here is show the causal diagram of motivation may look like:

Note that it includes both loops and “external”, confounding factors.

The criteria of sound research in medical or social sciences

Pearl teaches that any research in epidemiology, sociology, psychology, macroeconomy, and other medical and social sciences which back up their “findings” with statistics but don’t make clear the causal assumptions that they use and don’t perform corresponding sensitivity tests regarding these assumptions should be taken with a big grain of salt.

I think The Book of Why is a solid antidote to the ideas from this famous piece by Chris Anderson: “Correlation supersedes causation, and science can advance even without coherent models, unified theories, or really any mechanistic explanation at all.”

More ideas about causality and connections to other fields

Causal models are stored in human minds in reference frames

The idea that jumps out at me from The Book of Why is that the causal models are stored in human brains as reference frames (my speculation: mental reference frames of concepts have at most seven features), introduced in Jeff Hawkins in A Thousand Brains.

I think that in causal and counterfactual reasoning, humans use reference frames with caused-by (and causes) relationships:

Headache causes.

I think that there are no “horizontal”, mesh-like connections in reference frames of concepts, so I don’t think that human brains effectively store the causal diagrams as they are typically drawn:

However, the human brain can navigate such models by traversing a series of star-like reference frames with caused-by and causes relationships.

There is a related connection between The Book of Why and A Thousand Brains: Pearl writes that “causal explanations, not dry facts, make up the bulk of human knowledge”, which translates into Hawkins’ idea that “humans learn only within reference frames”.

Interventions are possible because causal mechanisms are assumed to be independent

When intervening in the causal diagram and the structural causal model of the system (situation, environment, etc.), why one is allowed to change just one or several functions (f_X) while leaving all other causal relationships and the functions for other variables intact? If one intervenes into one variable, for example, making patients take some medicine, what are the guarantees that some other things, not just the values of the variables causally dependent on the “Treatment” variable, but maybe relationships between other variables don’t change as well?

It turns out that such a guarantee is actually a requirement for a good causal model. In other words, if the decomposition (factorisation) of variables and causal effects between them is such that intervening into one variable actually changes other variables or their relationships in unpredictable ways, then such a decomposition cannot be called a causal model and the relationships between variables cannot be called causal relationships. This is called The Independent Causal Mechanisms Principle in [2].

For some reason, Pearl doesn’t discuss this important point in The Book of Why at all, despite he discusses mechanism autonomy (his term for mechanism independence; another term that is sometimes used for this property is invariance) in detail in his earlier book, Causality [6].

The Independent Causal Mechanisms Principle is just an assumption that human brains evolved to use

It’s important to remember that the Independent Causal Mechanisms Principle is merely a constraint on what a causal model is and not a universal principle of nature. Therefore, the principle shouldn’t be confused for being a physical (or metaphysical) feature of causality. However, I wouldn’t be surprised if there was a way to derive from first principles (physics, entropy) that some decomposition into independent causal mechanisms must be possible in most situations in some precise mathematical sense. Perhaps, this has even been done already because there seems to be quite a lot of papers connecting causality and entropy in various ways.

I think there are multiple reasons why human brains have evolved to assume causal mechanisms to be independent. First, the assumption often holds empirically, that is, there are ways to factorise most real-world situations, environments, systems, etc. into variables (features, factors, subsystems, etc.) and deduce causal mechanisms between these variables that are actually independent in the face of interventions. In most cases, human brains can also find such “good” causal factorisations quickly.

Second, human brains cannot store and reprocess a lot of past experiences in the face of new evidence, and, more generally, are slow and are not good at processing or learning from large quantities of data. Also, the memory capacity of human brains is limited. All this means that the only reasonable strategy for generalising learning across experiences and situations (including hypothetical situations that humans brains construct for their interventional and counterfactual reasoning) is to alter (or drop) only a handful of causal relationships (if not just one at a time) that they know about and to reuse all other knowledge as it is already stored. Compare to Small Mechanism Shift hypothesis from [2].

In 2021, machine intelligence is, in most cases, still a long road away from achieving humans’ level of robustness in reasoning and humans’ ability for generalisation, so AI researchers are following the evolution’s footsteps by incorporating causal reasoning with mechanism independence assumption into intelligence architectures. This assumption also makes causal inference cheaper computationally.

However, in the future, I think that machine intelligence might come up with some model architectures which move beyond the Independent Causal Mechanisms Principle to make better predictions in the context of complex systems (situations, environments, etc.). Complex systems are not a good fit for causal modelling as honed by the evolution and conceptualised by Pearl. See the next section:

How does causal modelling relate to the study of complex systems?

When a causal diagram contains loops which include the treatment and the effect variables, or worse so, if “everything depends on everything”, unless researchers are willing to sever all these loops by assuming that some causal links are weak and ignoring them (as noted above in the section “Back-door criterion”), the researchers should conclude that the system they are dealing with is complex (rather than merely complicated). All the methods of causal inference described by Pearl (back-door adjustment, front-door adjustment, counterfactual queries, mediation analysis) can’t yield provably correct results in such situations. These methods could still be useful, though, especially for sensitivity analysis (as described above), that is, estimating how complex the system really is.

This is why, in Dave Snowden’s Cynefin framework for decision-making, which categorises systems (contexts, environments, etc.) in four domains: clear, complicated, complex, and chaotic, the proper course of practical sense-making and decision-making action in complex and chaotic domains start requiring some intervention as the necessary first step: “probe-sense-respond” for complex systems and “act-sense-respond” for chaotic systems (while for complicated systems, it’s merely “sense-analyse-respond”, for example, using Pearl’s methods).

Causal inference as presented by Pearl in the book lives in the domain of mathematical science (i. e., the science governed by static equations), whereas making any predictions about complex systems is not imaginable without stepping into the realm of computational science, that is, making some simulations. Pearl makes a passing mention of sequential interventions and dynamic plans, the topic he discusses in more detail in [6].

Causality and systems thinking

There are several fairly obvious relationships between the practice of causal modelling and systems thinking.

First, a causal diagram of a system can be considered one of the types of system views, which are objects of attention in systems thinking: see the section “Make a causal model of an important system you are dealing with” above.

Second, per theory theory of cognition (and systems thinking is largely based on this theory) causal mechanisms essentially define functional roles of subsystems/elements in the systems.

References

[1] M. Eichler. Causal inference with multiple time series: principles and problems (2013)

[2] B. Schölkopf, F. Locatello et. al. Towards Causal Representation Learning (2021)

[3]. J. Pearl. The Causal Mediation Formula – A Guide to the Assessment of Pathways and Mechanisms (2011)

[4] D. Kenny. Mediation

[5] J. Wong. Computational Causal Inference (2020)

[6] J. Pearl. Causality: Models, Reasoning, and Inference (2009)